• 形形色色的图形数字问题补充

• 形形色色的图形数字问题再补充

• 叶军数学工作站第221期问题研究A另解答案的验证

• 图形图象中的数字问题一览

• 三次方程、三次函数、三个解

• 梁灶趣味数学题54

• 两道2020年年号题

• 梁灶趣味数学题30

• 梁灶趣味数学题18

• 梁灶趣味数学题3

• 十个数学问题的猜想

• 数学范畴之发展的新标志

• 鸢形

• 对元旦趣题的简单小结

• 平抑法证明不等式

• 与椭圆关联的几个有趣的同心圆

• 无穷对于有限认知的冲击

• 发现提炼于教学（讲座）

• 杨学枝猜想3及其姊妹不等式命题的证明及推广

• 棱线数及其应用举例

• 美国征解题的不同解法与引伸

• 利用函数性质证明一道数竞题

• 不定方程xy＋yz＋zx＝0的整数解及其他

• 关于《绝数表》的几个注记

• 解数学题的分步进行

• 椭圆平行弦的中点特征

• 谈谈函数作图

• 拓展意义上的尺规作图

• 一道数竞题的对偶思考

• 凸多边形的重心问题及其应用

• 一个数列求解通项中的数学思想及知识的蕴含

• 费波那契数的封闭特点

• 谈谈解析几何中的解题·编题·组题

• 从费波那契数列通项说起

• 重视例题教学的知识串联与变换技巧

• 成果集锦

• “资源重组”证明一类轮换对称不等式

叶军数学工作站第221期问题研究A另解答案的验证

重视例题教学的知识串联与变换技巧

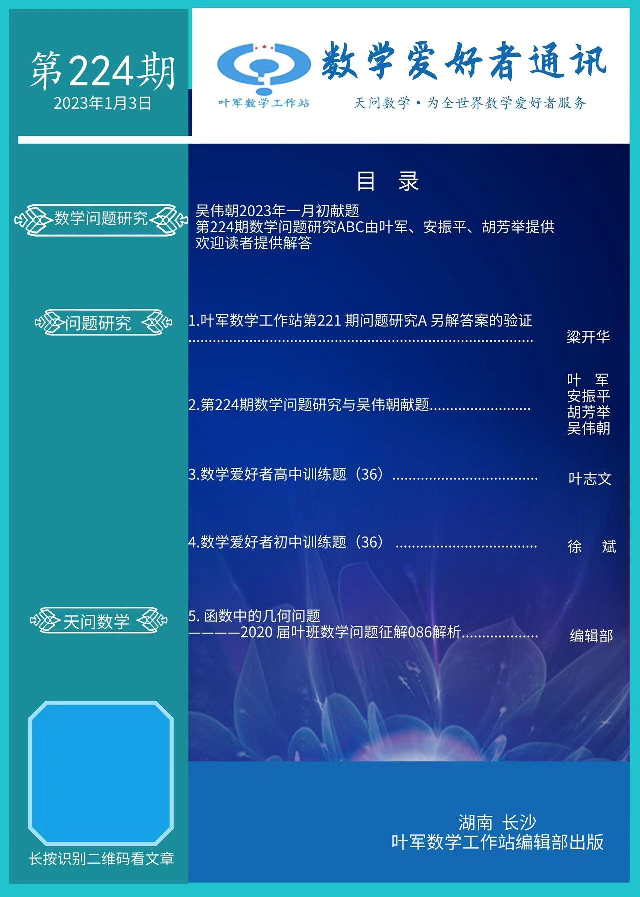
梁开华  《数学教学》1997（5）

    上海市新编数学教材有不少特色。其中明显的一条是基本的、重要的、典型的内容相对地集中了、突出了，特别是方法教学，比如高二数列一章，专门给出了“数列求和的几种方法”、“归纳—猜想—论证”等内容设置，变换训练的意图相当明显。现以该章中的例1为例，说明知识串联与技巧变换的教学设计及其迸发的数学美。

   （《数学高二年级第二学期》P95） 例1  顺次计算数列1，1+2+1，1+2+3+2+1，1+2+3+4+3+2+1，…的前4项的值，由此猜测a_n=1+2+3+…+（n-1）+n+（n-1）+…+3+2+1的结果，并用数学归纳法加以证明。

    分析与解：容易得出，1=1²，1+2+1=2²，1+2+3+2+1=3²,1+2+3+4+3+2+1=4²,

    从而猜测：a_n=1+2+3+…+（n-1）+n+（n-1）+…+3+2+1=n².

    用数学归纳法证明之：

（1）       当n=1的时，等式显然成立。

（2）       假设n=k时，等式成立，即a_k=k²,

则当n=k+1时，a_k+1=1+2+3+…+k+(k+1)+k+k-1+...+2+1=a_k+(k+1)+k=k²+2k+1=(k+1)² 。

等式也成立。

    综合（1）、（2），等式对任何n∈N都成立。

    这个题目的本身已蕴含理想的结构美，然而远非如此，我们来看下面的一串等式：

 1²=1，11²=121，111²=12321，…，11…1²=123…n…321                        (1)

                                                         n个

    例题的数列各项只不过是（1）所给出的（等号右边）数列各项的数字和。而这个数列各项(n²)的底数又恰恰是(等号左边)一系列的1相加所得的和。这真是天生般的自然美。

问题还在于这样的美的结构还具有明显的应用价值，只要我们注意串联对相关问题结构及其规律的观察与剖析。比如有这样一道因式分解题：

分解因式a⁴+2a³+3a²+2a+1

（1）的等号的右边，是不是已经隐含解答了呢？

解：原式=(a²+a+1)。

这又正是（1）抽象结构的具体化与应用化，且可用性的潜能大得很！

例2   试证数列10101，1010101，…，10101…01中的每一项都是合数（前苏联数学竞赛题）。

   分析与证明：我们不妨使命题的内容更充实些，也更一般些：

    设x=10，即证x⁴+x²+1，x⁶+x⁴+x²+1，…，x⁴ⁿ+x^4n-2+…+x²+1，x⁴ⁿ⁺²+x⁴ⁿ+…+x+1

始终能够因式分解。

    先解决其中的偶数项。每一项也总有偶数个项相加。把他们“拦腰”分作两部分，对一般形式，就有

  x⁴ⁿ⁺²+x⁴ⁿ+…+x²ⁿ⁺²+x²ⁿ+x^2n-2+…+x²+1

=x²ⁿ⁺²(x²ⁿ+x^2n-2+…+x²+1)+x²ⁿ+x^2n-2…+x²+1

=(x²ⁿ+x^2n-2+…+x²+1)(x²ⁿ⁺²+1)

    对于奇数项，先以一个简单式为过渡，体会解决的方法：

  x⁸+x⁶+x⁴+x²+1

=x⁸+2x⁶+3x⁴+2x²+1-(x⁶+2x⁴+x²)

=(x⁴+x²+1)²-(x³+x)²

=(x⁴+x³+x²+x+1)(x⁴-x³+x²-x+1)。

    于是，一般地，则有

  x⁴ⁿ+x^4n-2+…+x²ⁿ⁺²+x²ⁿ+x^2n-2+…+x²+1

=x⁴ⁿ+2x^4n-2+3x^4n-4+…+nx²ⁿ⁺²+(n+1)x²ⁿ+nx^2n-2+…2x²+1-(x^4n-2+2x^4n-4+…+(n-1)x²ⁿ⁺²+nx²ⁿ+(n-1)x^2n-2+…+2x⁴+x²)

=(x²ⁿ+x^2n-2+…+x²+1)²-(x^2n-1+x^2n-3+…+x³+x)²

=(x²ⁿ+x^2n-1+x^2n-2+…+x²+x+1)(x²ⁿ-x^2n-1+x^2n-2-…+x²-x+1)。

    代x=10，则表明数列

10101，1010101，…，10101…01中的每一项都是合数。

    课堂教学，特别是毕业班复习课，善于加强例题的知识串联与变换技巧，显然极其重要。这也是对教师的一种合理的但又较高的要求。

成果集锦

梁开华  《中学数学教学参考》2000（12）

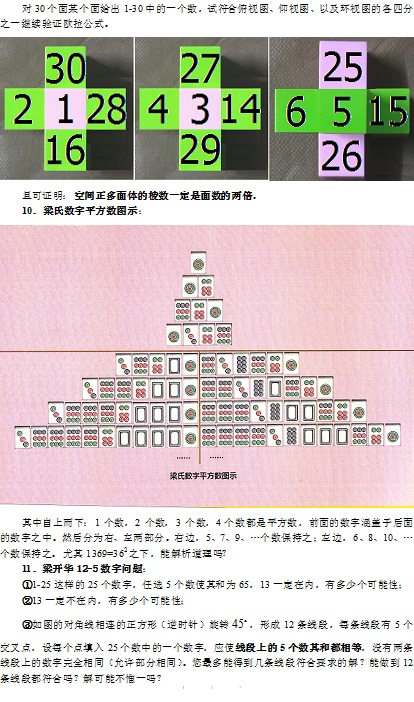
由三堆物博弈产生的一个有趣数阵

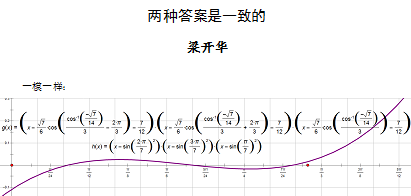
由个数分别为a、b、c的三堆物体中,甲乙轮流拿取:①每次可从任一堆中取走任意一个；②每次至少取一个；③每次只能从某一堆上取,不得从两堆或三堆上取.那么,谁取到最后一场,就算获胜.

这时,我们称数组(a,b,c)为一个局势,如果面对局势(a,b,c),甲先取,而乙有必胜策略,则称之为后发必胜局势, a、b、c称为一组绝数.如果记a_ii=0(i=1,2,…),a_i1=a,a_1j=b,a_ij=c,则(a、b、c)即可排成一个数阵{a_ij}

绝数数阵{a_ij}:

比如，取a=a₂₁=1,b=a₁₃=2,则c=a₂₃=3，于是(a,b,c)=（1，2，3）构成乙的必胜局势（无论甲怎样取，乙总有法获胜）。

该数阵的构成方法是：首行是0，1，2，…；第二行是首行的第一，第二两数对换，第三，四两数的对换…；第三行是第二行的每连续四个数倒排；第四行是第三行两两倒排；第五行是第四行的每连续八个数倒排…

这个数阵有非常丰富的性质：

⑴它是一个对称数阵，即a_ij=a_ji;

⑵每一行都是数0，1，2，3，…的某个排列;

⑶是以2ⁿ为模的模周期数阵；

 ⑷

     且有︳A₁ ︳=-1, ︳A₂ ︳=︳A₃ ︳=…=0；

 ⑸规定运算：10=01=1，11=00=0，将a,b,c都表成二进制数，则ab=c,bc=a,ca=b,如

a=14=1110_(2),b=11=1011₍₂₎,则c=1110₍₂₎+ 1011₍₂₎=101₍₂₎=5.

    绝数数阵有着丰富的性质和广泛应用，笔者已进行了初步开发。

 
“资源重组”证明一类轮换对称不等式

200333 上海晋元高级中学 梁开华

不等式证明以往是高中代数知识里比较重要的内容，由于证明方法特多，有时形成的解决办法很巧妙，因此颇为师生所感兴趣。其留给师生思索、探求的空间相当广阔，往往令人回味隽永，意蕴盎然。现在，在人们的感觉里，不等式证明的知识点不那么重要了；在上海，其淡化尤为显著。

但我认为，至少在拓展课或研究课里，进行不等式证明方法的探讨，依然值得考虑。不等式的表达形式中，轮换对称结构十分常见，证明方法也多得很。笔者这里介绍一种“资源重组”法，就是尽量用好平均的理念，把相关量的“多余”与“不足”进行重组与平衡，发挥“整体”的力量予以解决。

下面通过举例阐明这样方法的应用。

例1          x，y，z∈R⁺,

求证 

证明:    

其中 

    ∴ 原式

  ∴ 原不等式成立。

这个简单的例子里，把3/2分作3个1/2与每个关系式运算，把运算中间结果中含x－y的结构关联起来计算，这就是“资源重组法”的重要解法设计。相当一部分轮换对称的不等式证明，可以利用这个方法得到有效而令人满意地解决。

例2  x，y，z∈R⁺,

求证 

证明：

其中

    ∴ 原式

    ≤0。

∴ 原不等式成立。

例3  x，y，z∈R⁺,

求证

证明：即证

即

其中

∴ 原式=成立。

∴ 原不等式成立。

例4  a, b, c∈R⁺,

求证 

证明：即证

即

   .

其中

    ∴ 原式

成立。

∴ 原不等式成立。

通过以上举例可以体会笔者“资源重组法”用于不等式证明方法的简明与奥妙。遇到相关轮换对称不等式证明时，不妨先用本法一试。如果不够顺利或推证繁琐，再试用他法。

但不要以为这个方法所对应解决的不等式问题难度不大。上述有关例子有的已颇够份量。下面再举一个一般解法颇感头痛的例子。

例5          在锐角△ABC中，

求证  cosAcosB+cosBcosC+cosCcosA≤6sinA/2sinB/2sinC/2（题目取自2005．８．《数学通报·数学问题解答》题1563）。

证明：先给出一个熟知的结论：

在锐角△ABC中，cosA+cosB+cosC=1+4sinA/2sinB/2sinC/2.

∴ 12sinA/2sinB/2sinC/2=3(cosA+cosB+cosC)－3.

即证 3(cosA+cosB+cosC)－3－2(cosAcosB+cosBcosC+cosCcosA)≥0。

即证 (cosA－1)(1－2cosB)+(cosB－1)(1－2cosC)+(cosC－1)(1－2cosA)≥0。

左边

其中  

∴ 原式

=

∴ 原不等式成立。

本题的证明过程可充分领略重组资源结构配置转化的快乐。比之问题提供人给出的解法，用到一些特殊的图形结构及“车比雪夫不定式”等特殊结论，显然简明直接得多。另外，本题完整形式是

．．．求证cosAcosB+cosBcosC+cosCcosA≤6sinA/2sinB/2sinC/2≤sinA/2sinB/2+sinB/2sinC/2+sinC/2sinA/2.

右半结论原解法也不理想。不妨这样：

锐角△ABC中，

∴

这样多直截了当。